Answer:
,
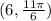
Explanation:
Note I'm using a, instead of theta to represent angles.
To convert rectangular to polar, apply these formulas
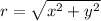

Note : Rectangular coordinates are the coordinates you were learning since elementary school or middle school.
The first number is x, and the second is y.
So
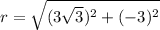
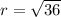
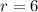
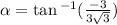
Since our y coordinate is negative and x coordinate is Positve , on the unit circle, the angle must be in the fourth quadrant.
So the angle must be in between
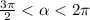
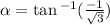
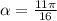
So our answer is
(6, 11pi/6).