Answer:
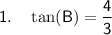
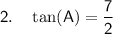
Explanation:
Acute angle: an angle less than 90°
Tan trigonometric ratio
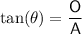
where:
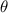 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
Question 1
Refer to the first attached diagram.
If tan(A) = 3/4 then the side opposite ∠A is 3 units, and the side adjacent ∠A is 4 units.
Therefore:
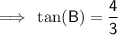
Question 2
Refer to the second attached diagram.
If tan(B) = 2/7 then the side opposite ∠B is ,and the side adjacent ∠B is 7.
Therefore:
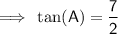
Question 3
Angle A would be bigger (see second attachment).