Question

The sum of three consecutive multiples of 7 is 693. Find the no​

Answer 1

Let x be a multiple of 7

• The next two consecutive multiples of 7 are x + 7 and x + 7 + 7 (i.e. x + 14)

Three consecutive multiples of 7 are

• x
• x + 7
• x + 14

According to the condition

`\\ \large\blue\longrightarrow\rm \large \:x \: + \: (x \: + \: 7) + (x \: + \: 14) \: = \: 693`

`\large\blue\longrightarrow \rm \large \:3x \: + \: 21 \: = \: 693`

`\large\blue\longrightarrow \rm \large \:3x \: = \: 693 \: - \: 21`

`\large\blue\longrightarrow \rm \large \:3x \: = \: 672`

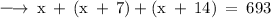
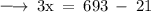
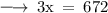
Dividing both sides by 3 , we have

`\large\blue\longrightarrow \rm \large \: (3x)/(3) \: = \: (672)/(3) \\`

`\large\blue\longrightarrow \rm \large \: \ \: ( \cancel3x)/( \cancel3) \: = \: \frac{ \cancel{672} \: \: ^{ \red{224}} }{ \cancel3} \\`

`\large\blue\longrightarrow \rm \large \:x \: = \: 224 \\`

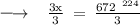
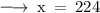
• x = 224
• x + 7 = 224 + 7 = 231
• x + 14 = 224 + 14 = 238

Three consecutive multiples of 7 are

• 224
• 231
• 238