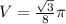Question

Considerar un sólido cuya base yace sobre el plano XY y está limitada por el eje X y por la curva y=sin(x), con 0≤x≤π12. Además, las secciones transversales, perpendiculares a la base y al eje X, son triángulos equiláteros. Entonces, el volumen del sólido es:

Answer 1

`V=(√(3))/(8)\pi`

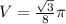
Explanation:

Para resolver este problema podemos comenzar haciendo un diagrama de cómo se vería un volumen diferencial en esta situación (ver imagen adjunta).

A partir de dicha imagen, podemos escribir una integral general que nos dirá como encontrar el volumen de toda la figura:

`V=\int\limits^\pi_0 {A_(T)} \, dx`

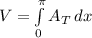
Para lo cual necesitamos encontrar una ecuación para el área del triángulo. Sabemos que el area de un triángulo está dada por:

`A_(T)=(bh)/(2)`

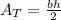
donde

b=base

h=altura

Ahora bien, como estamos hablando de triángulos equilateros, la altura puede reescribirse en términos de la base, haciendo uso de pitágoras, entonces obtenemos que:

`h=\sqrt{b^(2)-(b^(2))/(4)}`

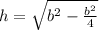
lo cual se puede simplificar:

`h=\sqrt{(3b^(2))/(4)}`

`h=(√(3))/(2)b`

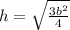
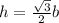
y esto a su vez puede ser sustituido en la ecuación del área:

`A=(√(3))/(4)b^(2)`

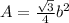
En este caso, sabemos que la base está limitada por el eje x y la curva y=sen(x) (asumo que es de
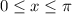`0\leq x \leq \pi`. Si los límites son distintos, lo único que cambia del procedimiento es eso, los límites de integración).

Entonces en este caso la base está dada por:

b=sen(x)

la cual puede ser sustituida en nuestra ecuación del área:

`A=(√(3))/(4)sen^(2)(x)`

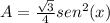
y esta a su vez puede ser sustituida en nuestra integral:

`V=\int\limits^\pi_0 {(√(3))/(4)sen^(2)(x)} \, dx`

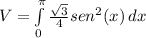
La cual puede ser simplificada:

`V=(√(3))/(4)\int\limits^\pi_0 {sen^(2)(x)} \, dx`

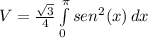
Y ya podemos integrar. Por identidades trigonométricas sabemos que:

`sen^(2)(x)=(1-cos(2x))/(2)`

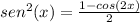
por lo que podemos sustituir la identidad en nuestra integral:

`V=(√(3))/(4)\int\limits^\pi_0 {(1-cos(2x))/(2)} \, dx`

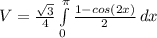
Y separarla en dos integrales:

`V=(√(3))/(4)(\int\limits^\pi_0 {(1)/(2)}-\int\limits^\pi_0 {(cos(2x))/(2)}) \, dx`

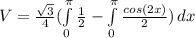
E integramos:

`V=(√(3))/(4)([(1)/(2)]^(\pi)_(0)-(1)/(4)[sen(u)]^(2\pi)_(0))`

Lo cual nos da de resultado:

`V=(√(3))/(4)((1)/(2)\pi-(1)/(2)(0)-(1)/(4)[sen(2\pi)-sen(0)])`

Y este se simplifica a:

`V=(√(3))/(8)\pi`