Answer:
They both represent the same equation
Explanation:
Given

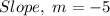
The question is not properly presented.
However, I can pick the following from the question.
Paul's workings:

Where
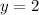
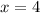 and
and
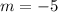
So:
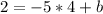
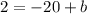


Seth's workings:

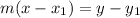
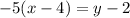
Required
Determine if both workings represent the same equation
Step 1: Analyze Paul's workings
Paul applied slope intercept to determine the equation of the line and his workings is correct.
Step 2: Analyze Seth's workings
Seth applied slope formula in determining the equation of the line and up till where Seth's stopped, Seth was correct.
The next step is to complete Seth's workings as follows:
Seth's workings:

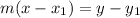
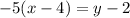
Open bracket
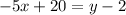
Collect Like Terms
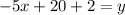
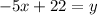
Reorder
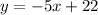
Comparing the end results of Seth and Paul's workings.
We have that both results are the same.
i.e.
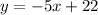
Hence, they both represent the same equation