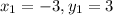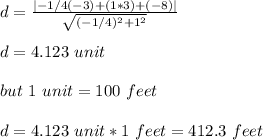Answer:
412.3 feet
Explanation:
A canoe rental shop is being built near a river. An equation of the line representing the river is y=1/4x+8. Each unit in the coordinate plane corresponds to 100 feet. Approximately how far is the canoe rental shop from the river? Round your answer to the nearest whole foot. The rental shop is at (-3,3).
Solution:
The distance between a point and a line is the perpendicular distance. The perpendicular distance is the shortest distance between the point and the line.
Given a point (
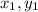 ) and a line with the equation Ax + By + C = 0, the perpendicular distance (d) is given as:
) and a line with the equation Ax + By + C = 0, the perpendicular distance (d) is given as:
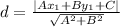
Given the equation of the line y = 1/4 x + 8
y - 1/4 x - 8 = 0
Therefore A = -1/4, B = 1 and C = -8
The point is (-3,3), therefore