Answer:
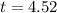
Explanation:
Given

Required
Time it hits the ground
When the object hits the ground, the height is 0.
In other words:
f(t) = 0
So, we have:
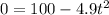
Collect like terms
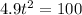
Divide through by 4.9
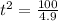
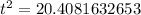
Take positive square roots of both sides
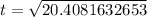
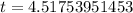
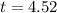
Hence, the ball hits the ground after 4.52 seconds