Question

Un topógrafo usa un instrumento llamado teodolito para medir el ángulo de elevación entre el nivel del piso y la cumbre de una montaña. En un punto, se mide un ángulo de elevación de 41°. Medio kilómetro más lejos de la base de la montaña, el ángulo de elevación medido es de 37°. ¿Qué altura tiene la montaña?

Answer 1

La altura de la montaña es 2848,80 m.

Explanation:

Un topógrafo usa un instrumento llamado teodolito para medir el ángulo de elevación entre el nivel del piso y la cumbre de una montaña. En un punto, se mide un ángulo de elevación de 41°.

La función trigonométrica tangente se define como:

`tan (angulo)=(cateto opuesto)/(cateto adyacente)`

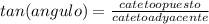
Entonces, siendo h altura de la montaña e y la distancia de la base de montaña a donde se realiza la medición, la distancia de esta primera observación del topógrafo entre el nivel del piso y la cumbre de una montaña es:

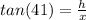`tan (41)=(h)/(x)` Ecuación (A)

Medio kilómetro más lejos de la base de la montaña, el ángulo de elevación medido es de 37°. Entonces:

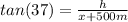`tan (37)=(h)/(x+500m)` Ecuación (B)

Entonces, despejando h de la ecuación (A):

h= tan(41)* x

Reemplazando la expresión en la ecuación (B):

`tan (37)=(tan(41)*x)/(x+500m)`

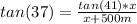
Resolviendo:

tan(37)*(x+500)= tan(41)* x

0,754*( X +500) = 0,869*X

0,754*X + 377 = 0,869*X

377= 0,869*X -0,754*X

377= 0,115*x

377÷0.115= x

x= 3278,26 m

Entonces, reemplazando en la expresión h= tan(41)* x:

h= tan(41)* 3278,26 m

Resolviendo:

h = 0,869 *3278.26 m

h = 2848,80 m

La altura de la montaña es 2848,80 m.

En la imagen adjunta se puede observar una representación gráfica de las medidas utilizadas en el problema.