Answer:
The polynomial function of the lowest degree that has zeroes at -1, 0 and 6 and with a leading coefficient of one is
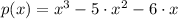 .
.
Explanation:
From Fundamental Theorem of Algebra, we remember that the degree of the polynomials determine the number of roots within. Since we know three roots, then the factorized form of the polynomial function with the lowest degree is:
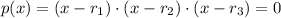 (1)
(1)
Where
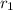 ,
,
 and
and
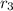 are the roots of the polynomial.
are the roots of the polynomial.
If we know that
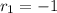 ,
,
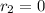 and
and
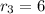 , then the polynomial function in factorized form is:
, then the polynomial function in factorized form is:
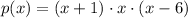 (2)
(2)
And by Algebra we get the standard form of the function:
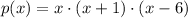
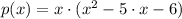
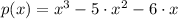 (3)
(3)
The polynomial function of the lowest degree that has zeroes at -1, 0 and 6 and with a leading coefficient of one is
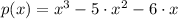 .
.