Question

If BTS=GHD BS=25 TS=14 BT=31 GD=4x-11 S=56 B=21 and H=(7y+5) find the values of x and y

Answer 1

Given:

Consider the completer question is "If ∆BTS≅∆GHD, BS=25, TS=14, BT=31, GD=4x-11, m∠S=56, m∠B=21 and m∠H=(7y+5), find the values of x and y.

To find:

The values of x and y.

Solution:

We have,

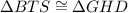`\Delta BTS\cong \Delta GHD` (Given)

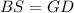`BS=GD` (CPCTC)

`25=4x-11`

`25+11=4x`

`36=4x`

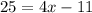
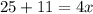
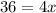
Divide both sides by 4.

`9=x`

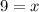
In ∆BTS,

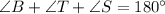`\angle B+\angle T+\angle S=180^\circ` (Angle sum property)

`21^\circ+\angle T+56^\circ=180^\circ`

`77^\circ+\angle T=180^\circ`

`\angle T=180^\circ-77^\circ`

`\angle T=103^\circ`

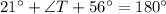
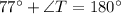
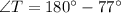
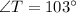
Now,

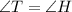`\angle T=\angle H` (CPCTC)

`103=7y+5`

`103-5=7y`

`98=7y`

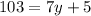
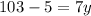
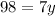
Divide both sides by 7.

`14=y`

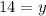
Therefore, the value of x is 9 and value of y is 14.