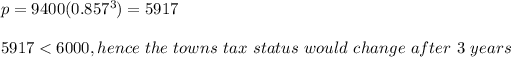Question

Select the correct answer from each drop-down menu. The population of a small town is decreasing exponentially at a rate of 14.3% each year. The current population is 9,400 people. The town's tax status will change once the population is below 6,000 people. Create an inequality that can be used to determine after how many years, t, the town's tax status will change, and use it to answer the question below. ()t < Will the town's tax status change within the next 3 years?

Answer 1

The answer is below

Explanation:

An exponential decrease can be represented by the formula:

`y=ab^x`

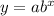
where a is the initial amount and b < 1.

Let p represent the population after t years, hence:

`p=ab^t`

Since the population decreases exponentially at a rate of 14.3% each year, hence:

b = 100% - 14.3% = 85.7% = 0.857

b = 0.857

Also, a = 9400 people

Therefore the equation is:

`p=9400(0.857^t)\\`

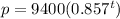
The town's tax status will change once the population is below 6,000 people, therefore:

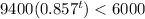`9400(0.857^t)<6000\\` for the tax status to change.

At t = 3 years:

`p=9400(0.857^3)=5917\\\\5917<6000,hence\ the\ towns\ tax\ status\ would \ change\ after\ 3\ years\\`