Answer:
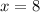
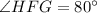
Explanation:
Given that:
Point
 is interior of
is interior of
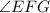 .
.

To find:
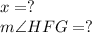
Solution:
First of all, let us represent the given values in the form of a diagram.
Kindly refer to the attached image for the given points and values of angles.
We can clearly see that:
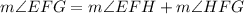
Putting all the values given in above equation, we get:

