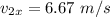Question

In Challenge Example 11.9 (p. 280), after the explosion, suppose that the m1 fragment shot directly north at 12 m/s and the m3 fragment shot directly south at 9 m/s. What would be the x-component of the velocity of the m2 fragment after the explosion

Answer 1

The question is incomplete. The mass of the object is 10 gram and travelling at a speed of 2 m/s.

Solution:

It is given that mass of object before explosion is,m = 10 g

Speed of object before explosion, v = 2 m/s

Let
`$m_1, m_2 \text{ and}\ m_3$` be the masses of the three fragments.

Let
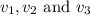`$v_1, v_2 \text{ and}\ v_3$` be the velocities of the three fragments.

Therefore, according to the law of conservation of momentum,

`$mv=m_1v_1 +m_2v_2+m_3v_3$`

`$10 * 2 \hat i=3 * 12 \hat{j} + 3(v_(2x) \hat{i}+v_(2y) \hat{j})-4 * 9 \hat{j}$`

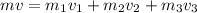
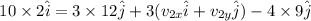
So the x- component of the velocity of the m2 fragment after the explosion is,

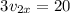
`$3v_(2x) = 20$`

∴
`$v_(2x) = 6.67 \ m/s$`