Solution :
Given initial velocity, v= 48 ft/s
Acceleration due to gravity, g =
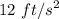
a). Therefore the maximum height he can jump on Mars is
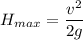
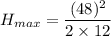
= 96 ft
b). Time he can stay in the air before hitting the ground is
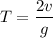
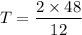
= 8 seconds
c). Considering upward motion as positive direction.
v = u + at
We find the time taken to reach the maximum height by taking v = 0.
v = u + at
0 = 16 + (12) t
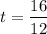

We know that,
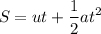
Taking t =
 , we get
, we get
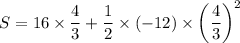
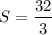 feet
feet
Thus he can't reach to 100 ft as it is shown in the movie.
d). For any jump whose final landing position will be same of the take off level, the final velocity will be the initial velocity.
Therefore final velocity is = -16 ft/s