Question

In major league soccer, standings are determined by points. Three points are awarded for each win, 1 point is awarded for each tie and 0 points are awarded for each loss. A major league soccer team finished the season with 55 points. They played 28 games and had 7 losses. Use matrix equations to solve for the number of wins and the number of ties the team had during the season. (a) State the coefficient matrix, the variable matrix and the constant matrix. (b) Solve the matrix equation to determine the number of wins and ties.

Answer 1

They won 17 games and drew 4 games

Explanation:

The given parameters are;

The number of points the major league soccer team finished with = 55 points

The number of games the soccer team played = 28 games

The number of losses the soccer team had = 7 losses

The number of points awarded for each win = 3 points

The number of points awarded for each tie = 1 points

The number of points awarded for each loss = 0 points

Let x represent the number of wins, y represent the number of draws, and let z represent the number losses

Therefore;

z = 7

x + y + z = 28

3·x + y + 7×0 = 55

Therefore, we have the following system of equations;

x + y = 21...(1)

3·x + y = 55...(2)

Which gives;

`\begin{bmatrix}1 & 1\\ 3 & 1\end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}21 \\ 55\end{bmatrix}`

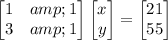
The inverse of the matrix is given as follows;

`(1)/(1 - 3) * \begin{bmatrix}1 & -3\\ -1 & 1\end{bmatrix} = \begin{bmatrix}-0.5 & 0.5\\ 1.5 & -0.5\end{bmatrix}`

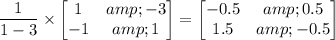
Therefore;

`\begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}-0.5 & 0.5\\ 1.5 & -0.5\end{bmatrix} * \begin{bmatrix}21 \\ 55\end{bmatrix} = \begin{bmatrix}17 \\ 4\end{bmatrix}`

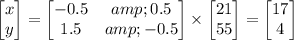
x = 17, y = 4