Answer:
The approximate angle of
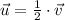 , where
, where
 , is 56º.
, is 56º.
Explanation:
Let
 and
and
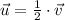 , then the resulting vector is described below:
, then the resulting vector is described below:
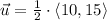
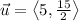
From Trigonometry, we find that direction angle of this vector is defined by the following inverse trigonometric expression:
 (1)
(1)
Where:
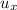 - x-Component of
- x-Component of
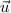 , dimensionless.
, dimensionless.
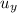 - y-Component of
- y-Component of
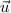 , dimensionless.
, dimensionless.
If we know that
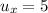 and
and
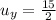 , then the direction angle of the vector is:
, then the direction angle of the vector is:
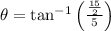

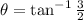
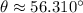
The approximate angle of
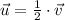 , where
, where
 , is 56º.
, is 56º.