The question is incomplete. The complete question is :
Many ancient tombs were cut from limestone rock that contained uranium. Since most such tombs are not well-ventilated, they may contain radon gas. In one study, the radon levels in a sample of 12 tombs in a particular region were measured in becquerels per cubic meter
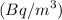 . For this data, assume that
. For this data, assume that
 and
and
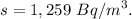 . Use this information to estimate, with 95% confidence, the mean level of radon exposure in tombs in the region. Interpret the resulting interval.
. Use this information to estimate, with 95% confidence, the mean level of radon exposure in tombs in the region. Interpret the resulting interval.
Solution :
Here, given
Mean sample,

Mean standard deviation ,
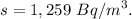 .
.
Sample size, n = 12
∴ Degree of freedom = n-1 = 12-1
= 11
Significance level, α = 0.05
The critical level,
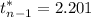
Therefore, lower limit =
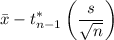
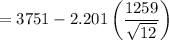
= 2951
Upper Limit =
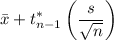
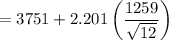
= 4551
Therefore the confidence interval is with 95 % and the true mean level of radon exposure in the tombs is between 2951
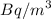 and 4551
and 4551
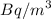 .
.