Question

Last night Mookie Betts hit a baseball at 32.5 m/s at a 45° angle. Betts

hit it from a height of 1m and the right field fence where he hit the ball

towards is 3m tall and 99m away. Was this hit a home run? How far did

it go?

Answer 1

a) Since the height of the baseball at 99 m was 8.93 m and the fence at that distance is 3m tall, the hit was a home run.

b) The total distance traveled by the baseball was 108.7 m.

Step-by-step explanation:

a) To know if the hit was a home run we need to calculate the height of the ball at 99 m:

`y_(f) = y_(0) + v_{0_(y)}t - (1)/(2)gt^(2)`

Where:

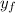`y_(f)`: is the final height =?

`y_(0)`: is the initial height = 1 m

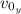`v_{0_(y)`: is the initial vertical velocity = v₀sin(45)

v₀: is the initial velocity = 32.5 m/s

g: is the gravity = 9.81 m/s²

t: is the time

First, we need to find the time by using the following equation:

`t = \frac{x}{v_{0_(x)}} = (99 m)/(32.5 m/s*cos(45)) = 4.31 s`

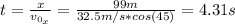
Now, the height is:

`y_(f) = y_(0) + v_{0_(y)}t - (1)/(2)gt^(2) = 1m + 32.5 m/s*sin(45)*4.31 s - (1)/(2)9.81 m/s^(2)*(4.31 s)^(2) = 8.93 m`

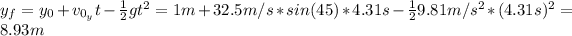
Since the height of the baseball at 99 m was 8.93 m and the fence at that distance is 3m tall, the hit was a home run.

b) To find the distance traveled by the baseball first we need to find the time of flight:

`y_(f) = y_(0) + v_{0_(y)}t - (1)/(2)gt^(2)`

`0 = 1 m + 32.5m/s*sin(45)t - (1)/(2)9.81 m/s^(2)t^(2)`

`1 m + 32.5m/s*sin(45)t - (1)/(2)9.81 m/s^(2)t^(2) = 0`

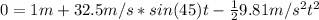
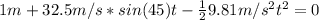
By solving the above quadratic equation we have:

t = 4.73 s

Finally, with that time we can find the distance traveled by the baseball:

`x = v_{0_(x)}*t = 32.5 m/s*cos(45)*4.73 s = 108.7 m`

Hence, the total distance traveled by the baseball was 108.7 m.

I hope it helps you!