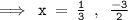Question

Factorise: 6 x2+ 7x -3

Answer 1

`{6x}^(2) + 7x - 3 \\ \\ {6x}^(2) + 9x - 2x - 3 \\ \\ ( {6x}^(2) + 9x) - (2x + 3) \\ \\ 3x(2x + 3) - 1(2x + 3) \\ \\ (3x - 1)(2x + 3).`

Answer 2

• Factoring a quadratic equation can be defined as the process of breaking the equation into the product of its factors.

`\:❏ \: \: \LARGE{\rm{{{\color{orange}{6 {x }^(2) \: + \: 7x \: - 3}}}}}`

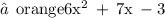
• Factorize the equation by breaking down the middle term.

`\large \blue\implies \tt \large \: 6 {x }^(2) \: + \: 7x \: - 3`

• Let’s identify two factors such that their sum is 7 and the product is -18.

Sum of two factors = 7 = 9 - 2

Product of these two factors = 9 × (-2) = 18

• Now, split the middle term.

`\large \blue\implies \tt \large \:6 {x}^(2) \: + \: 9x \: - \: 2x \: - \: 3`

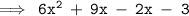
• Take the common terms and simplify.

`\: \\ \large\blue\implies \tt \large \:3x(2x \: + \: 3)\: -1(2x \: + \: 3)`

`\\ \large\blue\implies \tt \large \:(3x \: - \:1 ) \quad \: (2x \: + \: 3) \: = \: 0`

Thus, (3x - 1) and (2x + 3) are the factors of the given quadratic equation.

• Solving these two linear factors, we get

`\large\blue\implies \tt \large \:x \: = \: (1)/(3) \: \: , \: \: ( - 3)/(2) \\`