Question

Cos2A+cos2B+cos2C =–1–4cosAcosBcosC​

Answer 1

Explanation:

Hey there!

Given;

A+B+C = π

A+B = π-C (Take this)----->

B+C = π-A

A+C = π-B

Putting "sin" and "cos" on both sides. We get;

sin (A+B) = sin (π-C)

= sin C.....(i)

cos (A+B) = cos (π-C)

= -cos C......(ii)

Now, taking LHS. We get;

= cos (2A) + cos (2B) + cos (2C)

Use formula for cos (C) + cos (D) in first two terms.

`= 2. \cos( (2a + 2b)/(2) ). \cos( (2a - 2b)/(2) ) + \cos(2c)`

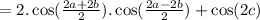
Simplify in first two terms. And keep cos (2C) in terms of cos. (i.e cos (2A) = 2cos^2 (A)-1).

= 2 cos (A+B). cos (A-B) + 2cos ^2(C)-1

Now, use (i).

`= - 2 \cos(c) . \cos(a - b ) + 2 { \cos}^(2) c - 1`

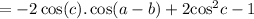
Take (-2cos (c)) common.

`= - 2 \cos(c) ( \cos(a - b) - \cos(c) ) - 1`

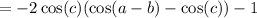
Use cos (C) = -cos(A+B).

`= - 2 \cos(c) ( \cos(a - b) . \cos(a + b) ) - 1`

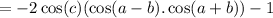
Use formula. (i.e cos (A+B) + cos (A-B) = 2.

= -1-4 cos (A) . cos (B). cos (C)

→ RHS proved.

Hope it helps....