Answer:
1) 288.8 km due North
2) 144.9 km due East
3) 323.1 km
4) 207°
Explanation:
Bearing: The angle (in degrees) measured clockwise from north.
Trigonometric ratios
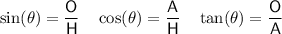
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
- H is the hypotenuse (the side opposite the right angle)
Cosine rule

where a, b and c are the sides and C is the angle opposite side c
-----------------------------------------------------------------------------------------------
Draw a diagram using the given information (see attached).
Create a right triangle (blue on attached diagram).
This right triangle can be used to calculate the additional vertical and horizontal distance the ship sailed after sailing north for 250 km.
Question 1
To find how far North the ship is now, find the measure of the short leg of the right triangle (labelled y on the attached diagram):
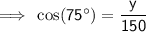

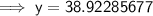
Then add it to the first portion of the journey:
⇒ 250 + 38.92285677... = 288.8 km
Therefore, the ship is now 288.8 km due North.
Question 2
To find how far East the ship is now, find the measure of the long leg of the right triangle (labelled x on the attached diagram):


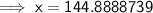
Therefore, the ship is now 144.9 km due East.
Question 3
To find how far the ship is from its starting point (labelled in red as d on the attached diagram), use the cosine rule:
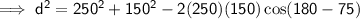
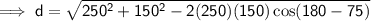
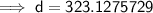
Therefore, the ship is 323.1 km from its starting point.
Question 4
To find the bearing that the ship is now from its original position, find the angle labelled green on the attached diagram.
Use the answers from part 1 and 2 to find the angle that needs to be added to 180°:

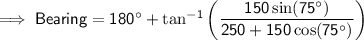
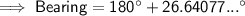

Therefore, as bearings are usually given as a three-figure bearings, the bearing of the ship from its original position is 207°