Question

The 60.0 kg skier shown below is skiing down a 35.0 degree incline where the magnitude of the friction force is 38.5N

a. what is the acceleration of the skier?
b. what is the normal force on the skier?

Answer 1

a) 4.98m/s²

b) 481.66N

Step-by-step explanation:

a) Using the Newtons second law of motion

`\sum F_x = ma_x\\F_m - F_f = ma_x\\Wsin \theta - F_f = ma_x\\mgsin \theta - F_f = ma_x\\`

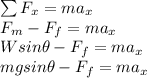
m is the mass of the object

g is the acceleration due to gravity

Fm is the moving force acting along the plane

Ff is the frictional force opposing the moving froce

a is the acceleration of the skier

Given

m = 60kg

g = 9.8m/s²

`\theta` = 35°

Ff = 38.5N

Required

acceleration of the skier a

Substituting into the formula;

`60(9.8)sin 35^0 - 38.5 = 60a\\588sin35^0 - 38.5 = 60a\\337.26 - 38.5 = 60a\\298.76 = 60a\\a = 298.76/60\\a = 4.98m/s^2\\`

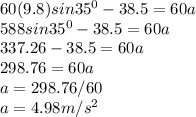
Hence the acceleration of the skier is 4.98m/s²

b) The normal force on the skier is expressed as;

N = Wcosθ

N = mgcosθ

N = 60(9.8)cos 35°

N = 588cos 35°

N = 481.66N

Hence the normal force on the skier is 481.66N