Answer:
Approximately
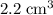 (assuming that this gas is ideal, and that the initial volume of this gas is
(assuming that this gas is ideal, and that the initial volume of this gas is
 .)
.)
Step-by-step explanation:
In this question, both the pressure on the gas and the temperature of the gas have changed. However, the ideal gas laws (Boyle's Law and Charles' Law) requires that only one of the two quantity change at a time. Therefore, consider this change in two steps:
- Change pressure from
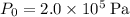 to
to
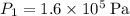 while keeping temperature constant at
while keeping temperature constant at
 . Find the new volume
. Find the new volume
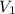 using Boyle's Law.
using Boyle's Law.
- After that, keep the pressure the same (at
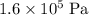 ) and change the temperature from
) and change the temperature from
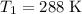 to
to
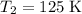 . Find the final volume of the gas
. Find the final volume of the gas
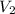 using Charles' Law.
using Charles' Law.
Boyle's Law states that for a fixed quantity of some ideal gas, if temperature is held constant, the volume of the gas will be inversely proportional to the pressure on the gas.
Let
 denote the initial volume of this gas. The question states that at
denote the initial volume of this gas. The question states that at
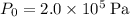 and
and
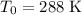 , the volume of the gas is
, the volume of the gas is
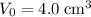 .
.
By Boyle's Law, if temperature is held constant (
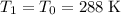 ,) then at
,) then at
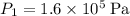 :
:
 .
.
On the other hand, Charles' Law suggests that for a fixed quantity of some ideal gas, if the pressure of the gas is held constant, the volume of the gas will be proportional to the temperature (in degree Kelvins) of the gas.
Let
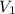 denote the volume of this gas before the temperature change. At
denote the volume of this gas before the temperature change. At
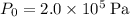 and
and
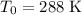 , previous calculations show that
, previous calculations show that
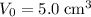 .
.
By Charles' Law, if the pressure of this gas is held constant (
 ,) then at the new temperature
,) then at the new temperature
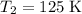 :
:
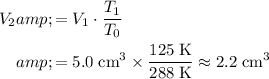 .
.
Therefore, at
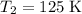 and
and
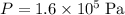 , the volume of this gas would be approximately
, the volume of this gas would be approximately
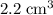 .
.