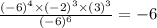Answer:
1)
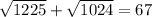
2)
![\sqrt[3]{-1331}=-11](https://img.qammunity.org/2021/formulas/mathematics/high-school/rm3t85w06yvgfntvs2fp1mfx5h154tcsgv.png)
3) Evaluating
 we get
we get
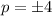
4)
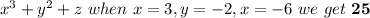
5)
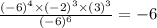
Explanation:
1)
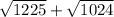
Prime factors of 1225 : 5x5x7x7
Prime factors of 1024: 2x2x2x2x2x2x2x2x2x2
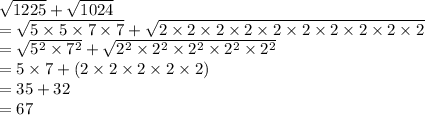
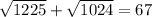
2)
![\sqrt[3]{-1331}](https://img.qammunity.org/2021/formulas/mathematics/high-school/i1cv68bwi2cxuan3f550vs799l0bq74x6t.png)
We know that
![\sqrt[n]{-x}=-\sqrt[n]{x} \ ( \ if \ n \ is \ odd)](https://img.qammunity.org/2021/formulas/mathematics/high-school/b15wm5ka8ugxzrcm9nkifus8lbek8n8vg6.png)
Applying radical rule:
![\sqrt[3]{-1331}\\=-\sqrt[3]{1331} \\=-\sqrt[3]{11*\11*11}\\=-\sqrt[3]{11^3} \\Using \ \sqrt[n]{x^n}=x \\=-11](https://img.qammunity.org/2021/formulas/mathematics/high-school/wushwaoar2zix1tlfk9x7obrwcvp7nbt73.png)
So,
![\sqrt[3]{-1331}=-11](https://img.qammunity.org/2021/formulas/mathematics/high-school/rm3t85w06yvgfntvs2fp1mfx5h154tcsgv.png)
3)

It can be written as:

Evaluating
 we get
we get
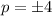
4)
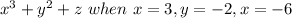
Put value of x, y and z in equation and solve:
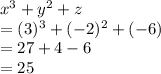
So,
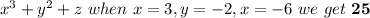
5)
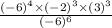
We know (-a)^n = (a)^n when n is even and (-a)^n = (-a)^n when n is odd
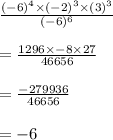
So,