Question

It is known that 10 workers take 30 days to complete a project. They start working and the next day one quits. the next another, the third day another, and so on until the sixth day when they are left alone 5 workers. How many days will it take those 5 workers to finish the job?​

Answer 1

5 workers finish this work in 60 days

Step by step explanation:

The problem tells us that at the end of the day, there are only 5 workers left, which we must find how many days it takes to finish said work.

We start by finding the type of proportionality we have.

In this case, we have that the more workers there are, they will finish that work in less time, and the fewer workers there are, the longer it will take to finish the work. This is the inverse proportionality, to more less, to less more.

We have only 5 workers left.

In the first case there are 10 workers, and in the second case there are 5 workers left. We find the relationship between the workers in the second case among the workers in the first case.

Ratio = 5 workers / 10 workers = 1/2

We see that the time is found by dividing the number of days in which the 10 workers finish the work, by 1/2.

As we know, dividing two fractions is the SAME as multiplying by the inverse fraction.

`\rm 30 * 2/1 \: = 60 \: days`

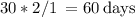
By so

5 workers finish this work in 60 days