Question

Amanda needs to make a garden plot which has an area less than 18 sq. feet. The length should be 3 feet longer than the width. What are the possible dimensions of the garden plot?

Answer 1

Any width less than 3 feet

Explanation:

Inequalities

The garden plot will have an area of less than 18 square feet. If L is the length of the garden plot and W is the width, the area is calculated by:

A = L.W

The first condition can be written as follows:

LW < 18

The length should be 3 feet longer than the width, thus:

L = W + 3

Substituting in the inequality:

(W + 3)W < 18

Operating and rearranging:

`W^2 + 3W - 18 < 0`

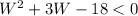
Factoring:

(W-3)(W+6)<0

Since W must be positive, the only restriction comes from:

W - 3 < 0

Or, equivalently:

W < 3

Since:

L = W + 3

W = L - 3

This means:

L - 3 < 3

L < 6

The width should be less than 3 feet and therefore the length will be less than 6 feet.

If the measures are whole numbers, the possible dimensions of the garden plot are:

W = 1 ft, L = 4 ft

W = 2 ft, L = 5 ft

Another solution would be (for non-integer numbers):

W = 2.5 ft, L = 5.5 ft

There are infinitely many possible combinations for W and L as real numbers.