Question

Q1 a) Kamahi invests some money which earns compound interest every year. His investment

amounts to sh60, 500 at the end of the second year and sh 73,205 at the end of the fourth year. Find
the rate of interest of the investment.
(5 marks)​

Answer 1

Without any more information, it sounds like interest is compounded continuously, in which case the value of the investment A is given by

`A=Pe^(rt)`

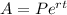
where P is the principal investment, r is the interest rate, and t is the number of years.

At the end of the second year (t = 2), the value is A = 60,500, and after the fourth year (t = 4), the value is A = 73,205. So solve the system

`\begin{cases}60,500=Pe^(2r)\\73,205=Pe^(4r)\end{cases}`

for r. You can eliminate P by dividing

`(Pe^(4r))/(Pe^(2r))=(73,205)/(60,500)\implies e^(2r)=(121)/(100)`

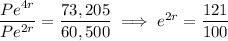
Take the logarithm (log here means natural log) of both sides to get

2r = log(121/100)

r = 1/2 log(121/100)

r ≈ 0.0953

So the interest rate is about 9.53%.

Answer 2

Answer: 2=2

Explanation: