Answer:
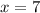
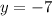
or
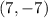
Explanation:
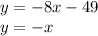
Begin by substituting
 for
for
 in the first equation given:
in the first equation given:
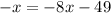
Add
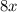 to both sides of the equation:
to both sides of the equation:
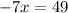
Divide both sides of the equation by the coefficient of
 , which is
, which is
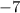 :
:
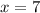
Now, substitute the
 value into the second equation given:
value into the second equation given:
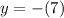
Distribute the negative:
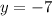
-
You can check your work by substituting the solved values into one of the given equations. Let's use the second one, as it will be easier to work with:
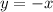
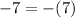
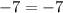
Since the sides of the equation are equal to each other, our solution is correct!