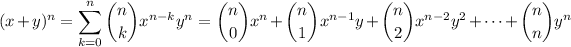Question

Expand each binomial.

14. (c - d)^7
15. (x+6)^6
16. (y-5)^7
17. (2a+4b)^4
18. (3a-4b)^5
19. (a-b)^6

we're supposed to use a table with three rows in our answers to solve this but i don't understand one bit. please help it's already a late assignment!
***the picture is how our answers should look!

Answer 1

See the attached image examples of some of the tables you would end up making.

In case you would like a more thorough explanation for all this:

Each term in the expansion of (x - 4)⁶ contributes (1) some power of x and (2) some power of -4. This is what's shown in the first two rows: descending powers of x and ascending powers of -4. Notice that the powers of x and -4 in the same column add up to 6. For example, x⁶ is paired with (-4)⁰, and x⁴ is paired with (-4)², and so on.

The third row contains what are called the binomial coefficients. These numbers tell you how many times the product in any given column shows up in the expansion. So (x - 4)⁶ contains 1 copy of x⁶(-4)⁰ = x⁶, 6 copies of x⁵(-4)¹ = -4x⁵, and so on.

Why do the powers sum to 6? Why are the coefficients 1, 6, 15, etc?

We can write

(x - 4)⁶ = (x - 4) (x - 4) (x - 4) (x - 4) (x - 4) (x - 4)

The powers sum to 6 because from the 6 copies of (x - 4) on the right, you will always pick between 0 and 6 copies of x and however many copies of -4 from the terms that don't provide an x.

For example, if we picked the highlighted terms here,

(x - 4) (x - 4) (x - 4) (x - 4) (x - 4) (x - 4)

then multiply them together, we get

x • x • x • x • x • (-4) = x⁵ (-4)¹ = -4x⁵

But there are 5 other ways to make this selection, including

(x - 4) (x - 4) (x - 4) (x - 4) (x - 4) (x - 4)

→ (-4) • x • x • x • x • x = -4x⁵

or

(x - 4) (x - 4) (x - 4) (x - 4) (x - 4) (x - 4)

→ x • x • x • (-4) • x • x = -4x⁵

and so on, giving a total of 6 possible choices of counting the product x⁵ (-4)¹.

The coefficients follow a pattern that can be arranged into what's known as Pascal's triangle:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

and so on. The n-th row of the array lists the coefficients in the expansion of (x + y)ⁿ, starting with n = 0. To demonstrate:

(x + y)⁰ = 1

(x + y)¹ = x + y = 1 x + 1 y

(x + y)² = x² + 2xy + y² = 1 x² + 2 xy + 1 y²

(x + y)³ = x³ + 3xy + 3xy + y³ = 1 x³ + 3 x²y + 3 xy² + 1 y³

and so on. For larger n, the pattern in the triangle continues by starting with 1 on the left, then adding together the two consecutive numbers in the previous row from above and to the left, then ending the new row with 1. For example, the next row for n = 5 would be

1 (1 + 4) (4 + 6) (6 + 4) (4 + 1) 1

or

1 5 10 10 5 1

and similarly, the next row for n = 6 would be

1 6 15 20 15 6 1

More generally, the k-th term in the n-th row, where 0 ≤ k ≤ n, is given a symbol (THE "binomial coefficient") defined as

`\dbinom nk=(n!)/(k!(n-k)!)`

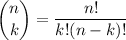
where ! denotes the factorial function, which shows up in what's known as the binomial theorem:

`(x+y)^n=\displaystyle\sum_(k=0)^n\binom nk x^(n-k) y^n=\binom n0x^n+\binom n1x^(n-1)y+\binom n2x^(n-2)y^2+\cdots+\binom nny^n`