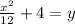Question

Consider the parabola with a focus at the point (0, 7) and directrix y = 1. Which two equations can be used to correctly relate the distances from the focus and the directrix to any point (x, y) on the parabola?

Answer 1

Explanation:

The equation that relates the distance from the focus and directrix to any point is

`(y - k) {}^(2) = 4p(x - h)`

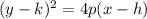
or

`(x - h) {}^(2) = 4p(y - k)`

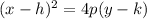
Since the directrix is a horizontal line, we will use the second equation.

The vertex lies halfway between the focus and directrix.

Since y=1, is perpendicular to the axis of symmetry, we are going to use the point (0,1) to represent the directrix.

Next, using the y values the number that lies between 7 and 1 is 4 so our vertex is

`(0,4)`

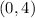
Our h is 0 and. k is 4.

`(x - 0) {}^(2) = 4p(y - 4)`

`{x}^(2) = 4p(y - 4)`

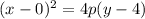
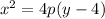
To find p, the equation of the focus is

`(h,k + p)`

`(0,4 + p)`

`4 + p = 7`

`p = 3`

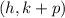
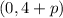
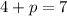
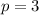
So we have

`{x}^(2) = 4(3)(y - 4)`

`{x}^(2) = 12(y - 4)`

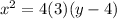
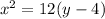
or

`\frac{ {x}^(2) }{12} + 4 = y`