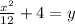Explanation:
The equation that relates the distance from the focus and directrix to any point is
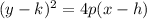
or
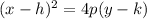
Since the directrix is a horizontal line, we will use the second equation.
The vertex lies halfway between the focus and directrix.
Since y=1, is perpendicular to the axis of symmetry, we are going to use the point (0,1) to represent the directrix.
Next, using the y values the number that lies between 7 and 1 is 4 so our vertex is
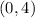
Our h is 0 and. k is 4.


To find p, the equation of the focus is
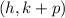
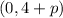
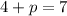
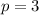
So we have

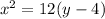
or