Answer:
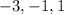 or
or
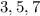
Explanation:
Let first consecutive odd integer =

Second consecutive odd integer =
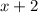
Third consecutive odd integer =
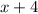
"Product of the first two is equal to one more than twice the third" can be written as:
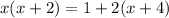
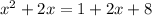 (expand brackets)
(expand brackets)
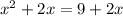 (combine like terms)
(combine like terms)
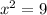

∴ Consecutive integers =
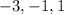 or
or
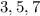
Hope this helps :)