The calculated solution
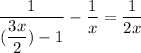 to the equation for the variable x is x = 1.2
to the equation for the variable x is x = 1.2
How to determine the solution to the equation
From the question, we have the following parameters that can be used in our computation:
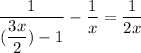
Add 1/x to both sides of the equation
So, we have

Evaluate the equation
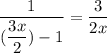
Take the inverse of both sides
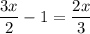
Collect the like terms
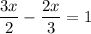
So, we have
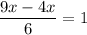
Next, we have
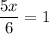
Cross multiply
5x = 6
Divide both sides by 5
x = 6/5
Evaluate
x = 1.2
Hence, the solution to the equation is x = 1.2