Explanation:
Use the difference quotient
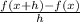
Here it will become
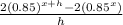
For the first box, let x=-4, and h= 0.001
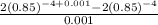
Using a calculator, you will get about
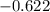
Next, let do this for 0.5
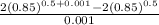
You will get about
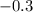
Finally, do this for
1.25
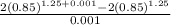
You get about
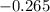
Note : This is the definition of a derivative