Question

Find the distance between (3,4) and (4,-6) if necessary, round to the nearest tenth.

Answer 1

The distance is:

d = 10.0 units (Rounded to the nearest the Tenths Place)

Explanation:

Given the points

• (3,4)

• (4,-6)

The distance 'd' between (3,4) and (4,-6)

`\mathrm{Compute\:the\:distance\:between\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):`

`d=√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

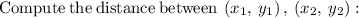
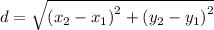
substituting the points values

`=√(\left(4-3\right)^2+\left(-6-4\right)^2)`

`=√(1+10^2)`

`=√(1+100)`

`=√(101)`

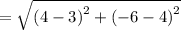
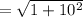
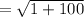
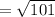
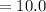`=10.0` units (Rounded to the nearest the Tenths Place)

Thus, the distance is:

d = 10.0 units (Rounded to the nearest the Tenths Place)