Question

~~~~25 POINTS!!~~~~PLEASE HELP~~~~~~

Given tan(0)=5/6, then cos(0)=a/b. Determine the values of a and b

Answer 1

Value of a= 6

Value of b= 7.81

Explanation:

We are given
`tan \theta=(5)/(6)`

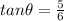
and
`cos \theta=(a)/(b)`

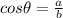
We need to find values of a and b

We know that:
`tan \theta=(Perpendicular)/(Base)`

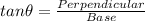
While
`cos \theta = (Base)/(Hypotenuse)`

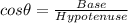
So, a = Base and b= Hypotenuse

We know the value of base i,e
`tan \theta=(Perpendicular)/(Base)=(5)/(6)`

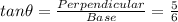
We get Base=6, Perpendicular = 5

To find Hypotenuse we can use Pythagoras theorem

`(H)^2=(P)^2+(B)^2\\H^2=(5)^2+(6)^2\\H^2=25+36\\H^2=61\\H=√(61)\\H=7.81`

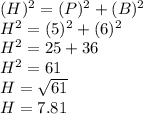
The value of hypotenuse is 7.81

The value of Base is 6

So,
`cos \theta = (Base)/(Hypotenuse) =(a)/(b)= (6)/(7.81)`

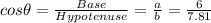
Value of a= 6

Value of b= 7.81