Question

Write equation of the line containing (4,2) and (3,5)
in slope-intercept form.

Answer 1

The equation of the line containing (4,2) and (3,5) in the slope-intercept form will be:

• y=-3x+14

Explanation:

Given the points

• (4, 2)

• (3, 5)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(4,\:2\right),\:\left(x_2,\:y_2\right)=\left(3,\:5\right)`

`m=(5-2)/(3-4)`

`m=-3`

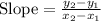
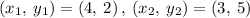
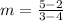
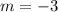
We know that the slope-intercept form of the line equation is

`y=mx+b`

where m is the slope and b is the y-intercept

substituting m=-3 and the point (4, 2) to get the y-intercept i.e. b

`y=mx+b`

2=(-3)4 + b

2 = -12 + b

b = 2+12

b = 14

Now, substituting b=14 and m=-3 in the slope-intercept form to determine the equation of a line in the slope-intercept.

`y=mx+b`

y=(-3)x+(14)

y=-3x+14

Thus, the equation of the line containing (4,2) and (3,5) in the slope-intercept form will be:

• y=-3x+14