9514 1404 393
Answer:
(2.27, 0.96)
Explanation:
The orthocenter is the point of intersection of altitudes of the triangle. The equation for an altitude is the equation of a line through a vertex that is perpendicular to the opposite side.
For example, the line perpendicular to side AC can be found as ...
(∆x, ∆y) = C-A = (3, -1) -(-4, 2) = (7, -3)
∆x(x -h) +∆y(y -k) = 0 . . . . perpendicular through point (h, k)
For side AC, we want the point to be B(4, 5), so the equation is ...
7(x -4) -3(y -5) = 0
7x -3y -13 = 0
Similarly, the altitude to side AB can be written as ...
(∆x, ∆y) = B -A = (4, 5) -(-4, 2) = (8, 3)
8(x -3) +3(y +1) = 0
8x +3y -21 = 0
__
By the "cross multiplication method", the solution to these equations is ...
x = (-3(-21) -(3(-13))/(7(3) -8(-3)) = (63+39)/(21+24) = 102/45 = 2 4/15 ≈ 2.27
y = (-13(8) -(-21)(7))/45 = 43/45 ≈ 0.96
The orthocenter is near (2.27, 0.96).
__
A graphing application confirms this result.
_____
Additional information about the cross multiplication method
For the general form equations ...
- ax +by +c = 0
- dx +ey +g = 0
The "cross multiplication method" has you write the array ...
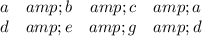
and form the "cross products" in groups of four coefficients:
D = ae -db, X = bg -ec, Y = cd -ga
Then the solution to the set of equations is ...
1/D = x/X = y/Y ⇒ x = X/D, y = Y/D
__
Additional note
Videos of this method show you writing the array as bcab/egde and using the final equation x/X=y/Y=1/D. The above gets the same result in a more straightforward manner.