Answer:
The equation of the quadratic graph is y =
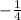 (x - 3)²
(x - 3)²
Explanation:
The standard form of the equation of the quadratic graph is
(x - h)² = 4p(y - k), where
- The vertex of the parabola is (h, k)
- The directrix is at y = k - p
∵ The focus is (3, -1)
∵ The focus is (h, k + p)
→ Compare them
∴ h = 3
∴ k + p = -1 ⇒ (1)
∵ The directrix is at y = 1
∵ The directrix is at y = k - p
→ Compare them
∴ k - p = 1 ⇒ (2)
→ Add equations (1) and (2) to eliminate p
∵ (k + k) + (p - p) = (-1 + 1)
∴ 2k + 0 = 0
∴ 2k = 0
→ Divide both sides by 2
∴ K = 0
→ Substitute the value of k in equation (1) to find p
∵ 0 + p = -1
∴ p = -1
→ Substitute the values of h, k, and p in the form of the equation above
∵ (x - 3)² = 4(-1)(y - 0)
∴ (x - 3)² = -4(y)
∴ (x - 3)² = -4y
→ Divide both sides by -4
∴
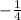 (x - 3)² = y
(x - 3)² = y
→ Switch the two sides
∴ y =
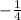 (x - 3)²
(x - 3)²
∴ The equation of the quadratic graph is y =
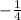 (x - 3)²
(x - 3)²