Answer:

Step-by-step explanation:
First, find the molar mass of H₂S
Use the Periodic Table to find the mass of hydrogen and sulfur.
- Hydrogen (H): 1.008 g/mol
- Sulfur (S): 32.07 g/mol
To find the molar mass of H₂S, multiply the molar mass of the elements by the number of atoms of the element.
- Hydrogen (2): (2)(1.008 g/mol) =2.016 g/mol
- Sulfur (1 atom): (1)(32.07 g/mol)= 32.07 g/mol
Add.
- 2.016 g/mol + 32.07 g/mol =34.086 g/mol
Next, find the number of moles in the sample (252.3 g) Use the ratio of grams to moles.
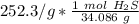
Multiply. The grams will cancel each other out.
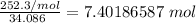
Finally, found the number of molecules using Avogadro's number (There are 6.022*10²³ molecules in 1 mole).
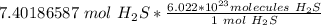
Multiply. The mole (mol) will cancel each other out.
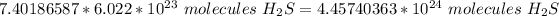
Round to the correct number of significant figures. The sample had 4 sig figs (2, 5, 2, 3), so round to 4 sig figs.
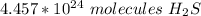
There are about 4.457 * 10²⁴ molecules of H₂S