Question

At the indicated point find (a) the slope of the curve and (b) an equation of the tangent line.

f(x)= 6x at (-2,-3)

Answer 1

Slope of the Curve:
`f'(x)=(-6)/(x^2)`

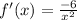
Equation of Tangent Line: y + 3 = -3/2(x + 2)

General Formulas and Concepts:

Pre-Algebra

• Order of Operations: BPEMDAS

Algebra I

Point-Slope Form: y - y₁ = m(x - x₁)

• x₁ - x coordinate
• y₁ - y coordinate
• m - slope

Calculus

The definition of a derivative is the slope of the tangent line.

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Quotient Rule:
`(d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Explanation:

Step 1: Define

`f(x)=(6)/(x)`

Step 2: Take Derivative

1. Quotient Rule:
   `f'(x)=(0(x)-6(1))/(x^2)`
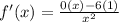
2. Multiply:
   `f'(x)=(0-6)/(x^2)`
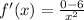
3. Subtract:
   `f'(x)=(-6)/(x^2)`

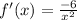
Step 3: Find Instantaneous Derivative

1. Substitute in x:
   `f'(x)=(-6)/((-2)^2)`
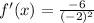
2. Exponents:
   `f'(x)=(-6)/(4)`
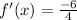
3. Simplify:
   `f'(x)=(-3)/(2)`

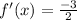
This value shows the slope of the tangent line at the exact value of x = 2.

1. Substitute: y + 3 = -3/2(x + 2)