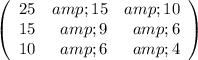Question

Find the resultant matrix ~


`\begin{gathered} \begin{bmatrix} {5 } \\ 3 \\ 2 \\ \end{bmatrix}\end{gathered} * \begin{gathered} \begin{bmatrix} {5 } \: \: \: 3 \: \: \: 2 \\ \end{bmatrix}\end{gathered}`
​

Answer 1

`\begin{gathered}\left[\begin{array}{ccc}5\\3\\2\end{array}\right] *[5 \ \ \ 3 \ \ \ 2]\end{gathered} \\ \\ \begin{gathered}\bf{\left( \begin{array}{rrr} 5 \\ 3 \\ 2 \end{array}\right) \ \ (5 \ \ 3 \ \ 2)}\end{gathered}`

`\begin{gathered}\bf{ \left( \begin{array}{rrr} 5*5 & 5*3 & 5*2 \\ 3*5 & 3*3 & 3*2 \\ 2*5 & 2*3 & 2*2 \end{array}\right) }\end{gathered}`

`\begin{gathered}\left( \begin{array}{rrr} 25 & 15 & 10 \\ 15 & 9 & 6 \\ 10 & 6 & 4 \end{array}\right)\end{gathered}`

Answer 2

`\left[\begin{array}{ccc}5\\3\\2\end{array}\right] *[5 \ \ \ 3 \ \ \ 2]`

Matrix multiplications are defined if the number of columns in the first matrix is equal to the number of rows in the second matrix.

`\bf{\left( \begin{array}{rrr} 5 \\ 3 \\ 2 \end{array}\right) \ \ (5 \ \ 3 \ \ 2)}`

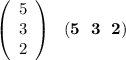
Multiply the first element of the array by the first element of the second array to get the element of the first row of the first column in the product array.

`\bf{\left( \begin{array}{rrr} 5*5 & & \\ & & \\ & & \end{array}\right)}`

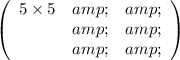
The remaining elements of the product matrix are obtained in the same way.

`\bf{ \left( \begin{array}{rrr} 5*5 & 5*3 & 5*2 \\ 3*5 & 3*3 & 3*2 \\ 2*5 & 2*3 & 2*2 \end{array}\right) }`

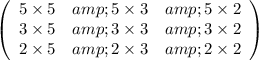
Simplify each item by multiplying the individual terms.

`\left( \begin{array}{rrr} 25 & 15 & 10 \\ 15 & 9 & 6 \\ 10 & 6 & 4 \end{array}\right)`

`\huge \red{\boxed{\green{\boxed{\boldsymbol{\purple{Pisces04}}}}}}`