Question

The pH of a 0.15 M butylamine, C&H3NH2 solution is 12.0 at 25°C. Calculate the dissociation

constant of the base.​

Answer 1

The dissociation constant of the base : 7.4 x 10⁻⁴

Further explanation

Butylamine, C4H9NH2 Is A Weak Base

Kb is the dissociation constant of the base.​

LOH (aq) ---> L⁺ (aq) + OH⁻ (aq)

`\rm Kb=([L][OH^-])/([LOH])`

[OH⁻] for weak base can be formulated :

`\tt [OH^-]=√(Kb.M)`

pH of solution : 12

pH+pOH=14, so pOH :

14-12 = 2, then :

`\tt [OH^-]=10^(-pOH)\\\\(OH^-]=10^(-2)`

the the dissociation constant (Kb) =

`\tt 10^(-2)=√(Kb.0.15)\\\\10^(-4)=Kb* 0.15\\\\Kb=(10^(-4))/(0.15)=6.6* 10^(-4)`

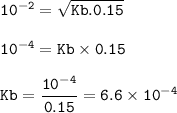
Or you can use from ICE method :

C4H9NH2(aq) + H2O(l) ⇌ C4H9NH3+(aq) + OH-(aq)

0.15

x x x

0.15-x x x

`\tt Kb=(x^2)/(0.15-x)\rightarrow x=[OH^-]\\\\Kb=(10^(-4))/(0.15-10^(-2))=7.14* 10^(-4)`