Question

Prove that -


`\sin {}^(2) (\theta) + \cos { }^(2) (\theta ) = 1`

thankyou! ~​

Answer 1

Depends.

If you defined
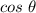`cos\ \theta` and
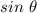`sin\ \theta` based on the unit circle, as in the coordinates of the point at a distance of
`\theta` from the point
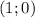`(1;0)` measured counterclockwise along the circle, then. it's proven by the fact that since that points sit on a circle of center the origin and radius 1, it's coordinates needs to satisfy the equation
`x^2+y^2 = 1`.

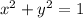If you define them based on right triangles, as in the ratios between adjacent (cosine) or oppsite (sine) sides and the hypotenuse, then it's simply applying the Pythagorean theorem. In particular let a be the hypotenuse of a right triangle of which one of the angles measures
`\theta`, let b the adjacent side to said angle, and c the opposite side.

By definition,
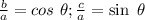`\frac ba = cos\ \theta ; \frac ca = \sin\ \theta`. clearing denominators we get
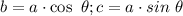`b= a\cdot\cos\ \theta; c= a\cdot sin\ \theta`, and applying the Pythagorean theorem:

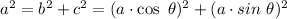`a^2= b^2+c^2 = (a\cdot\cos\ \theta)^2 + (a\cdot sin\ \theta)^2` And, taking the first and last step in this chain, dividing everything by
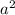`a^2` which is obviously non-zero we're left with
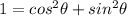`1= cos^2\theta + sin^2\theta`, QED.