Answer:
It will take 43.15 minutes for the lake and the tank to contain the same amount of water.
Explanation:
Given that:
Water tank contains 12.3 gallons of water.
1.6 gallons per minute are being added by Mark.
Let,
m be the minutes in which water tank is filling.
T(m) = 1.6m + 12.3
The lake has 98.6 gallons of water.
Water is drained at a rate of 0.4 gallons per minute.
L(m) = -0.4m + 98.6
For same amount of water,
T(m) = L(m)
1.6m+12.3 = -0.4m+98.6
1.6m+0.4m = 98.6 -12.3
2.0m = 86.3
Dividing both sides by 2
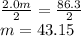
Hence,
It will take 43.15 minutes for the lake and the tank to contain the same amount of water.