Answer:
5.06
Explanation:
Given that the remaining credit after 38 minutes of calls is 19.68, and the remaining credit after 60 minutes of calls is 12.20.
As the credit remaining on a phone card (in dollars) is a linear function of the total calling time made with the card (in minutes), so let the linear equation be

where y is the credit remaining on a phone card (in dollars) and x is the total calling time made with the card (in minutes).
Now, as the remaining credit after 38 minutes of calls is 19.68, so, put x=38 and y=19.68 in equation (i), we have
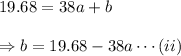
Similarly, the remaining credit after 60 minutes of calls is 12.20, so, put x=60 and y=12.20 in equation (i), we have
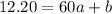
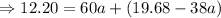 [ by using (ii)]
[ by using (ii)]
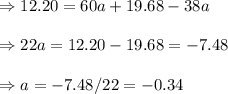
From equation (ii),
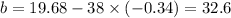
Putting the value od a and b in equation (i), we have
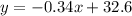
So, the remaining credit after 81 minutes can be determined by putting x=81 in the above equation.
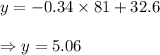
Hence, the remaining credit after 81 minutes of calls is $5.06.