Answer:



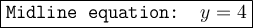
Explanation:
This is a trigonometric function which can be graphed. The function, much like others, contains valuable information on the qualities of the graph. Generally, trigonometric functions in this form are in the following format:
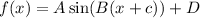
Where..
- A is the amplitude factor
- B is the period (
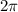 divided by it)
divided by it) - C is the horizontal shift left
- D is the vertical shift (midline)
Using this information, we can find the following information.
AMPLITUDE
To find the amplitude of this function, we can simply use the A term of the equation as that multiplies the maximum and minimum by that value.
In the equation
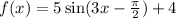 , the number 5 is at the A term.
, the number 5 is at the A term.
Thus, the amplitude of this graph is 5.
PERIOD
To find the period of the graph, we use the B term of the equation, then divide
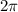 by this term as our regular period. Using this information and the equation, we know that our B term is 3. We can now divide.
by this term as our regular period. Using this information and the equation, we know that our B term is 3. We can now divide.
MIDLINE
Much like the amplitude, a simple value on this function gives us the midline. The D term of the equation gives us the midline as it shifts the function up/down after all is finished. Looking at the equation, the D term is 4. Since this shifts the function up, we know we're looking at a change in the y-axis.
Thus, the equation of the midline is
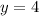
Hope this helped!