Question

.Find the inverse of A if it has one, or state that the inverse does not exist.

Answer 1

Explanation:

Find the discriminant

`|a| = ad - bc`

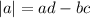
for a matrix

(a b)

(c d)

Here it is

`( - 6)( - 2) - 0(5)`

`12 - 0 = 12`

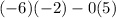
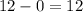
The formula for the inverse of a 2 by 2 matrix,

`(1)/(ad - bc) \binom{d}{ - c} \binom{ - b}{a}`

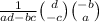
Note since the discriminant isn't 0, an inverse must exist.

`(1)/(12) \binom{ - 2}{ - 5} \binom{ 0}{ - 6}`

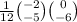
Multiply everything by the fraction.

`\binom{ - (1)/(6) }{ ( - 5)/(12) } \binom{ 0 }{ - (1)/(2) }`

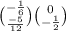
The last matrix is the inverse of A