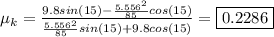Hello!
a)
For a car on an incline, we only have the normal force and force of gravity acting on the car.
The car is only experiencing a net force caused by the sine component of the force of gravity vector, which causes it to slide down the incline towards the center of the curve.
Or, as an equation:
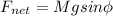
This net force produces a centripetal force. Recall the equation for centripetal force:
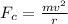
In reference to the 15° angle of the incline, the cosine component of the centripetal force is equivalent to the sine component of the force due to gravity (both parallel to the incline). So:
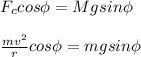
Cancel out 'm' and solve for 'v'.
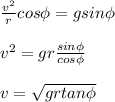
Plug in the given values and solve.
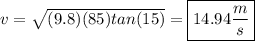
b)
Begin by converting 20.0 km/h to m/s.
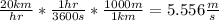
For this situation, we also have the force of friction present along the axis of the sine component of the force of gravity that contributes to the net force.
Recall the equation of kinetic friction:
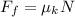
In this situation, we have the sine (vertical) component of the centripetal force as well as the cosine component of the force of gravity making up the normal force, so:
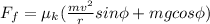
If a curve is banked at a slower speed than appropriate, the car will tend to slide towards the center. Thus, this force of friction points up the incline, opposite to the force due to gravity. We can do another summation of forces like above.
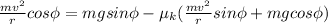
Cancel out 'm' and simplify the equation further to solve for μ.
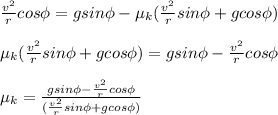
Plug in values.