Answer:
Approximately
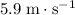 (assuming that the partner is holding the other end of the coil stationary.)
(assuming that the partner is holding the other end of the coil stationary.)
Step-by-step explanation:
In a standing wave, an antinode is a point that moves with maximal amplitude, while a node is a point that does not move at all. There is an antinode between every two adjacent nodes. Likewise, there is a node between every two adjacent antinodes.
The side of the spring that is being shaken moving with maximal amplitude. Hence, that point on this spring would also be an antinode. In contrast, the side of the spring that is held still (does not move at all) would be a node.
There would be a node between:
- the antinode at the end of the spring that is being shaken, and
- the antinode between the two ends of this spring.
Overall, the nodes and antinodes on this spring would be:
- node at the end that is being held still,
- antinode (as mentioned in the question),
- node (inferred, not mentioned in the question), and
- antinode at the end that is being shaken.
The distance between two adjacent nodes is equal to one-half (that is,
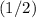 ) the wavelength of the wave. The distance between a node and an adjacent antinode is one-quarter (that is,
) the wavelength of the wave. The distance between a node and an adjacent antinode is one-quarter (that is,
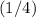 ) of the wavelength of the wave.
) of the wavelength of the wave.
Thus, if the wavelength of the wave in this question is
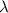 , the length of this spring would be:
, the length of this spring would be:
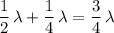 .
.
The question states that the length of this coiled spring is
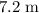 . In other words,
. In other words,
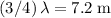 . The wavelength of this wave would be
. The wavelength of this wave would be
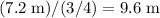 .
.
The frequency
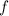 of this wave is the number of cycles in unit time:
of this wave is the number of cycles in unit time:
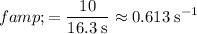 .
.
Hence, the speed
 of this wave would be:
of this wave would be:
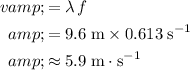 .
.